二叉树的递归遍历空间复杂度为 O(logN) 问题

在阅读《程序员面试代码指南 第 2 版》的第二章的 “将搜索二叉树转换成双向链表” 这一节时，书中有一个递归的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public ReturnType process(Node head) {
    if (head == null) {
        return new ReturnType(null, null);
    }
    ReturnType leftList = process(head.left);
    ReturnType rightList = process(head.right);
    if (leftList.end != null) {
        leftList.end.right = head;
    }
    head.left = leftList.end;
    head.right = rightList.start;
    if (rightList.start != null) {
        rightList.start.left = head;
    }
    return new ReturnType(leftList.start != null ? leftList.start : head, rightList.end != null ? rightList.end : head);
}

这段代码的作用是使用递归的方法嫁给你二叉搜索树转换成双向链表。

书中有这样一句话来描述其空间复杂度

process 递归函数最多占用二叉树高度为 h 的栈空间，所以额外空间复杂度为 O(h)。

这里的 \(O(h)\) 即 \(O(logN)\)，其中，\(N\) 为二叉树的节点个数。

一开始我并不理解为什么空间复杂度是 \(O(logN)\)，后来几经周折，终于想通。遂记录之。

我们可以这样理解，一个函数调用栈就是一个 “空间单位”，然后我们这个递归函数即使是调用到二叉树的最下面的一层，所耗费的函数调用栈的个数也不会超过 \(logN\)，因此，这个递归调用的空间复杂度是 \(O(logN)\)。

这里要注意一个误区，就是不要在计算函数调用栈的时候把函数执行过程中从头到尾的所有调用栈的数量认为是所耗费的空间数量。事实上，我们只需要函数执行到当前这一步时，程序所耗费的调用栈。我们可以把函数调用栈等价成一个 int 变量来理解，int 变量在程序执行的过程中可能会被重新赋值，但是，一个单个的 int 变量，无论它在程序执行的过程中被重新赋值多少次，它所占的空间始终是只有一个固定的数量，而不应该在每一次这个 int 值变化的时候都把它所占的空间再加一遍。

我们借助 IDEA 的调试工具看一下函数调用栈来加深理解

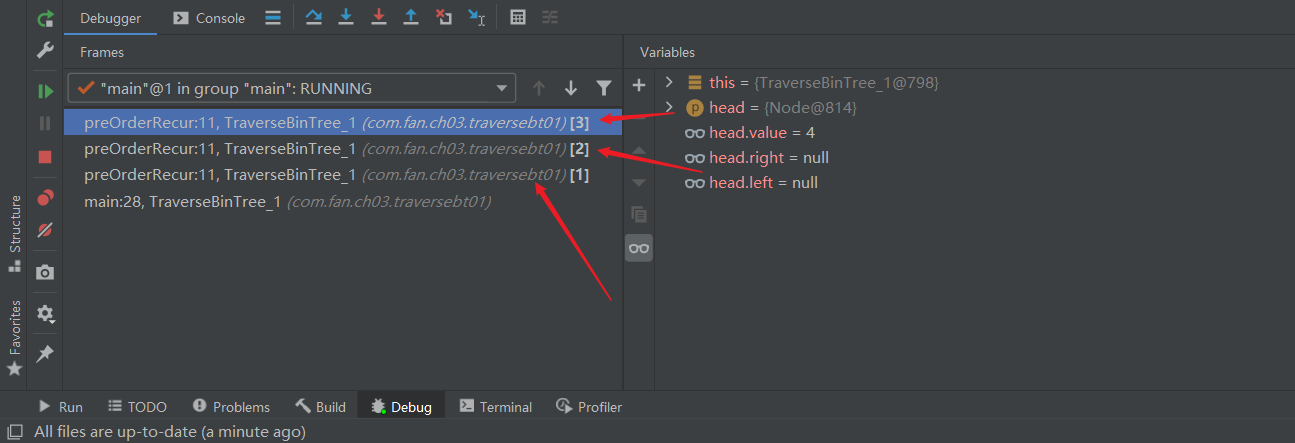
20210326192112

上图是一个二叉树的递归先序遍历，同时遍历到达最后一层时的递归调用栈。